P7146: 正确答案
传统题
1.000s
时间限制
256MB
内存限制
2 提交
1 解决
【题目描述】
【题目背景】某次测验后,信奥老师在黑板上留下了一串数字 23333 便飘然而去。凝望着这个神秘数字,小智同学不禁陷入了沉思……
【题目描述】
已知某次测验包含 n 道单项选择题,其中第 i 题(1≤i≤n)有 ai 个选项,正确选项为 bi,满足 ai≥2 且 0≤bi<ai。比如说,ai=4 表示第 i 题有 4 个选项,此时正确选项 bi 的取值一定是 0、1、2、3 其中之一。
信奥老师设计了如下方式对正确答案进行编码,使得仅用一个整数 m 便可表示 b1,b2,⋯,bn。
首先定义一个辅助数组 ci,表示数组 ai 的前缀乘积。当 1≤i≤n 时,满足:ci=a1×a2×...×ai
特别地,定义c0=1。
于是 m 便可按照如下公式算出:
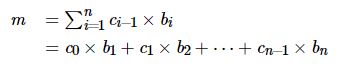
易知,0≤m<cn,最小值和最大值分别当 bi 全部为 0 和 bi=ai−1 时取得。
试帮助小智同学,把测验的正确答案 b1,b2,⋯,bn 从老师留下的神秘整数 m 中恢复出来。
【输入格式】
输入共两行。
第一行包含用空格分隔的两个整数 n 和 m,分别表示题目数量和老师的神秘数字。
第二行包含用空格分隔的 n 个整数 a1,a2,⋯,an,依次表示每道选择题的选项数目。
【输出格式】
输出仅一行,包含用空格分隔的 n 个整数 b1,b2,⋯,bn,依次表示每道选择题的正确选项。
【样例1输入】
15 32767
2 2 2 2 2 2 2 2 2 2 2 2 2 2 2
【样例1输出】
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
【样例2输入】
4 0
2 3 2 5
【样例2输出】
0 0 0 0
【样例3输入】
7 23333
3 5 20 10 4 3 10
【样例3输出】
2 2 15 7 3 1 0
【样例3解释】
i 1 2 3 4 5 6 7
ai 3 5 20 10 4 3 10
bi 2 2 15 7 3 1 0
ci−1 1 3 15 300 3000 12000 36000
【子任务】
50% 的测试数据满足:ai 全部等于 2,即每道题均只有两个选项,此时 ci=2i;
全部的测试数据满足:1≤n≤20,ai≥2 且 cn≤109(根据题目描述中的定义 cn 表示全部 ai 的乘积)。
【提示】
对任意的 1≤j≤n,因为 cj+1,cj+2,⋯ 均为 cj 的倍数,所以 m 除以 cj 的余数具有如下性质:
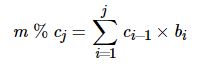
其中 % 表示取余运算。令 j 取不同的值,则有如下等式:
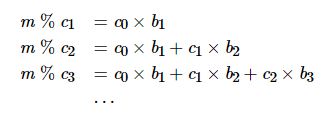
【样例输入】复制
7 23333 3 5 20 10 4 3 10
【样例输出】 复制
2 2 15 7 3 1 0