P5108: 吃西瓜-【2021暑期训练】T3Day2T2
【题目描述】
吃西瓜【问题描述】
老胡买了是长方体形的西瓜来犒劳大家....
这块西瓜长m厘米,宽n厘米,高h厘米.他发现如果把这块西瓜平均地分成m*n*h块1立方厘米的小正方体,那么每一小块都会有一个营养值(可能为负,因为西瓜是有可能坏掉的,但是绝对值不超过200)。
现在老胡决定从这m*n*h立方厘米的西瓜中切出mm*nn*hh(0<=mm<=m,0<=nn<=n,0<=hh<=h)立方厘米的一块小西瓜(一定是立方体形,长宽高均为整数),送给该场比赛最高分获得者补充营养。他想知道他最多能获得多少营养值。
换句话说,我们希望从一个m*n*h的三维矩阵中,找出一个三维子矩阵,这个子矩阵的权和最大.
一个2*3*4的例子,最优方案为切红色2*3*1部分。
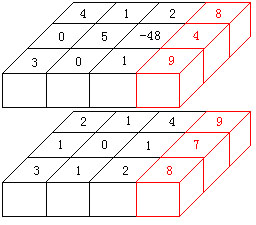
【文件输入】matrix.in
首行三个正整数h,m,n(注意顺序),分别表示西瓜的高,长,宽.
以下h部分,每部分是一个m*n的矩阵,第i部分第j行的第k个数表示西瓜第i层,第j行第k列的那块1立方厘米的小正方体的营养值.
【文件输出】matrix.out
老胡所能得到的最大营养值
【输入输出样例】
|
matrix.in
|
matrix.out
|
|
2 3 4
4 1 2 8 0 5 -48 4 3 0 1 9 2 1 4 9 1 0 1 7 3 1 2 8 |
45
|
对于30%的数据,h=1,1<=m,n<=10
对于全部的数据,1<=h<=32,1<=m,n<=50,保证h<=m,n
[说明]此题中出现的所有数全为整数。
【样例输入】复制
【样例输出】 复制
【提示】
首先考虑一个问题:最大连续和.
比如一个数列
3 -2 3 -5 6 9 要在这个数列中找出连续的一段(一个),使得它的和最大.对于这个数列来说,是6+9=15.
这里提供一个O(n)的算法:维护一个域sum,然后扫描数列,令sum不停地加a[i],当sum>ans时记录下来,当sum<0时将sum赋成0.
比如对于上面那个数列,初始sum为0.
第一个数为3,sum=3.
第二个数为-2,sum=1
第三个数为3,sum=4
第四个数为-5,sum=-1,sum<0,所以令sum=0
第5个数为6,sum=6
第6个数为9,sum=15.
以上过程中,sum的最大值15即是答案.
然后推广到二维:求最大子矩阵.这一类题有很多,比如vijos1255.
O(n^3)的算法是:枚举左右边界,然后求最大连续和.预处理O(n^3),求的过程O(n^3).预处理的过程,是事先求出每一行从第i列到第j列的和.
当然,预处理和求的过程可以放在一起.下面就是一段O(n^3)的代码:
For i:=1 to n do
Begin
For
j:=1 to m do f[i]:=0;
For j:=I to n
do
Begin
For k:=1 to m do inc(f[k],a[k,j]);
Sum:=0;
For k:=1 to m do
Begin
Inc(sum,f[k]);
If sum>ans then ans:=sum;
If sum<0 then sum:=0
End
End
End;
当你了解这个思想之后,就很容易推广到三维了.利用枚举加优化可以达到O(n^5)的算法---
思路1 枚举左右边界,枚举前后边界,然后求最大连续和,O(n^2*m^2*h),能通过70%数据
思路2 枚举左右边界,枚举上下边界,然后求最大连续和,O(n^2*h^2*m),能通过100%数据
思路3 枚举前后边界,枚举上下边界,然后求最大连续和.O(m^2*h^2*n),能通过100%数据.
这里希望引起用思路1的大牛们的思考:同样是O(n^5)算法,为什么少得30分?
原因:h<m,n,所以O(n^2*m^2*h)耗时高于O(n^2*h^2*m).
所以希望大家通过数据范围正确地选择算法